キャンペーンの詳細に関しましては、バナーをクリックしてください
2011年12月 6日
覚えておきたい数学の小技
数学の指導に役立つ小技を集めてみました。
覚えなければ数学が解けないというものではありませんが、特に数学が苦手な生徒には覚えておいて欲しい小技たちです。記事の中で役立ちそうな小技があったら、是非生徒に紹介してあげて下さい
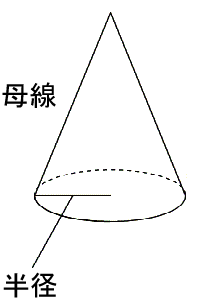
円錐の側面積の公式
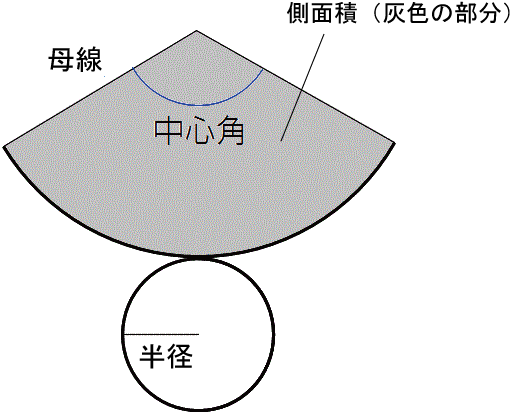
円錐の側面積は、底面の周の長さと側面の円の弧の長さの比から中心角を割り出して、求めることができます。
しかし、手順として少々煩雑
で、数学が苦手な子には教えるのがとっても大変です。
そんな時は、以下の公式を覚えておくと便利です。
円錐の側面積（上図の灰色の部分）＝ 母線の長さ×半径×π
意外に簡単な形なので、覚えてもらってもそんなに苦にはならないと思いますよ
×25の扱い方
88×25と言われて、皆さんはどう計算しますか
普通に筆算で解こうとすると結構ややこしいですよね
しかし、×25を見方を変えて、
×100/4と捉えるとどうでしょう。
88×25 = 88×100/4
= 22×100
= 2200 
意外に簡単に解けるでしょ
最大公約数・最小公倍数
連除法という方法があります。これを使うと、簡単に最大公約数と最小公倍数を求めることができます。下記は、連除法で54と72を2つ同時に計算した式です。
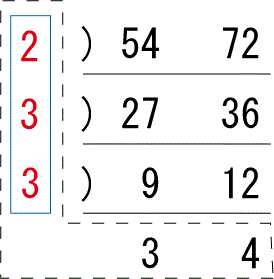
＜最大公約数の求め方＞
上の式の左側の数字を全て掛け合わせると求めることができます。ここでは、2×3×3=18 が最大公約数となります。
＜最小公倍数の求め方＞
点線で囲まれた全ての数字を掛け合わせると求めることができます。ここでは、2×3×3×3×4= 216 が最小公倍数となります。
分数の通分の時によく使う最小公倍数。中学生でも最小公倍数を求めることが苦手な生徒は結構います。教えている生徒が分数の通分を苦手にしていたら、是非教えてあげて下さい。
座標平面上の三角形の面積の求め方
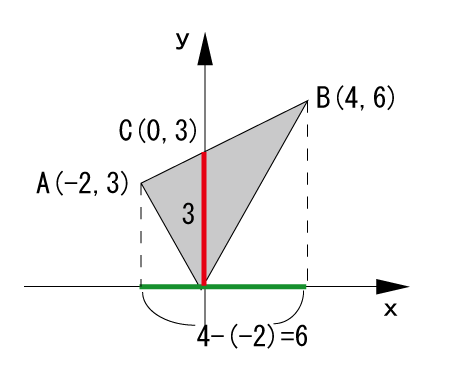
下図のように3つの頂点の座標が既知で、三角形の一つの頂点が原点にあり、三角形とy軸との交点（y切片）が分かっている場合に使えるテクニックです
三角形の面積 = 2頂点のx軸方向の距離(緑の線の長さ)×y切片(赤の線の長さ)×1/2
となります。
上図でどうしてそうなるかをご説明します。y軸で三角形を2つに分けて、y切片を底辺とした三角形が2つあると見れば、求められることが分かりますよね！
ちなみに上図の三角形の面積を求めると、
三角形の面積 = 6(x軸方向の距離)×3(y切片)×1/2 = 9
となります。
この小技は、2次関数のと直線の交点を結んで得られる三角形の面積を求める問題で使えると思います。
ダイヤグラムの問題での傾きの捉え方
縦軸(y軸)に距離、横軸(x軸)に時間を取ったグラフをダイヤグラムと言います。ダイヤグラムを使った問題は、公立高校の入試では頻繁に取り扱われる問題で、以下の点を抑えておくと、点数が取りやすくなると思います。
・グラフの傾きの絶対値が速さを表す！
当たり前すぎることですが、しっかり教え込んで、「傾き（の絶対値)が大きいと言うことは歩くスピードが速いってことをだよ」と伝えましょう。また、分速20mで、、、、と言われれば、即 y=20x+b のかたちになるということも伝えましょう。
平方根の大小
代表的な√の値は暗記させましょう。
√2 = 1.41421356 (一夜一夜に人見ごろ)
√3 = 1.7320508 (人なみにおごれや)
√5 = 2.2360679 (富士山麓オウム鳴く)
√6 = 2.44949 (似よ、よくよく)
√7 = 2.6457 (（菜）に虫いない)
√8 = 2.828427 (ニヤニヤ呼ぶな)
√5までは必須。√6から√8はできたら覚えさせましょう。√5から√8までは約0.2ずつ上がっているということを覚えてもらうだけでも良いと思います。
本記事は、「塾技100」(森圭示著・文英堂)を参照して作成しました。
- 塾で教える高校入試 数学 塾技100/森 圭示
- ￥1,575
- Amazon.co.jp
@kogamouse
